Learning to Approximate Adaptive Kernel Convolution on Graphs

Jaeyoon Sim1, Sooyeon Jeon1, InJun Choi1, Guorong Wu2, Won Hwa Kim1
1POSTECH, 2UNC-Chapel Hill

AAAI 2024

:canada: Vancouver, Canada

Paper arXiv Poster Code

Illustration of overall framework (LSAP).

This video shows how LSAP learns adaptive scales on the brain network (graph) for each node
corresponding to a specific ROI during 2000 epochs using ADNI dataset. After training, all
four models can obtain node-wise scales, but the three LSAP models using approximation
are ~10 times faster to learn the scales than Exact under the same conditions.

Abstract

Various Graph Neural Networks (GNNs) have been successful in analyzing data in non-Euclidean spaces, however, they have limitations such as oversmoothing, i.e., information becomes excessively averaged as the number of hidden layers increases. The issue stems from the intrinsic formulation of conventional graph convolution where the nodal features are aggregated from a direct neighborhood per layer across the entire nodes in the graph. As setting different number of hid- den layers per node is infeasible, recent works leverage a diffusion kernel to redefine the graph structure and incorporate information from farther nodes. Unfortunately, such approaches suffer from heavy diagonalization of a graph Laplacian or learning a large transform matrix. In this regards, we propose a diffusion learning framework where the range of feature aggregation is controlled by the scale of a diffusion kernel. For efficient computation, we derive closed-form derivatives of approximations of the graph convolution with respect to the scale, so that node-wise range can be adaptively learned. With a downstream classifier, the entire framework is made trainable in an end-to-end manner. Our model is tested on various standard datasets for node-wise classification for the state-of-the-art performance, and it is also validated on a real-world brain network data for graph classifications to demonstrate its practicality for Alzheimer classification.

Quantative Results

Node Classification

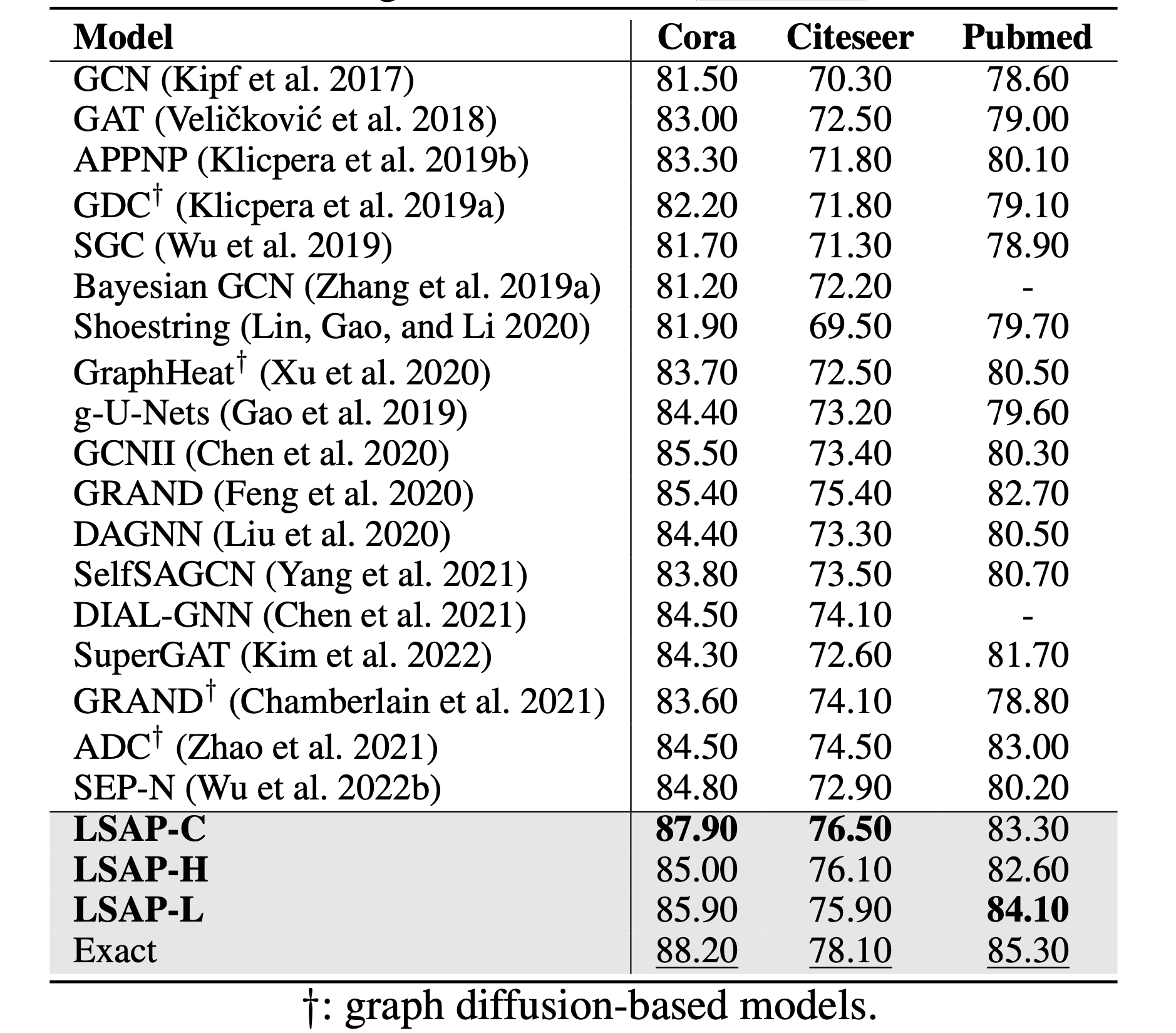
Table: Accuracy (%) on standard benchmarks for node classification. LSAP yields better performances over existing baselines (in bold) similar to Exact achieving the best results (underline).

Graph Classification

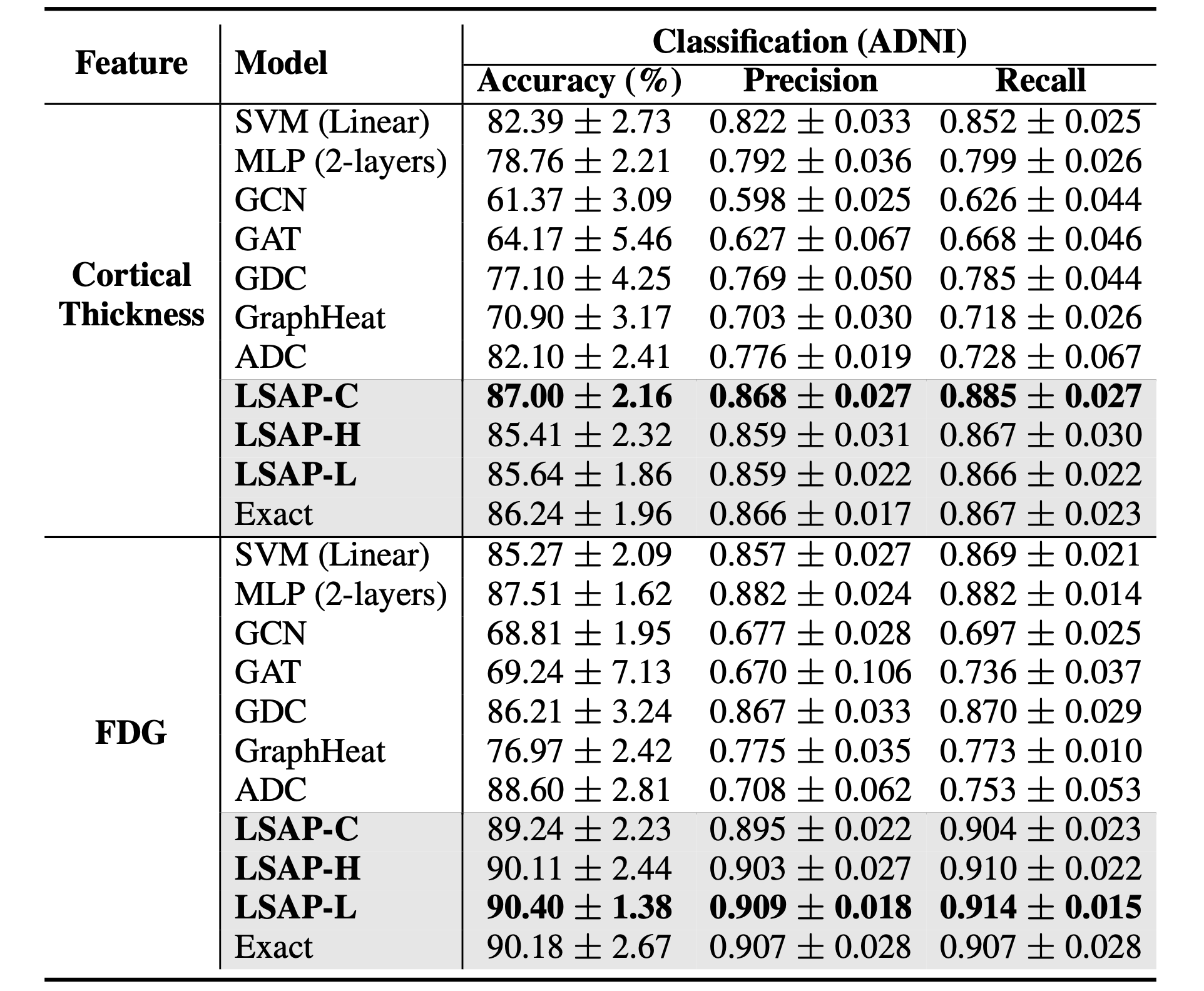
Table: Classification performances on ADNI dataset (for CN / SMC/ EMCI / LMCI / AD).

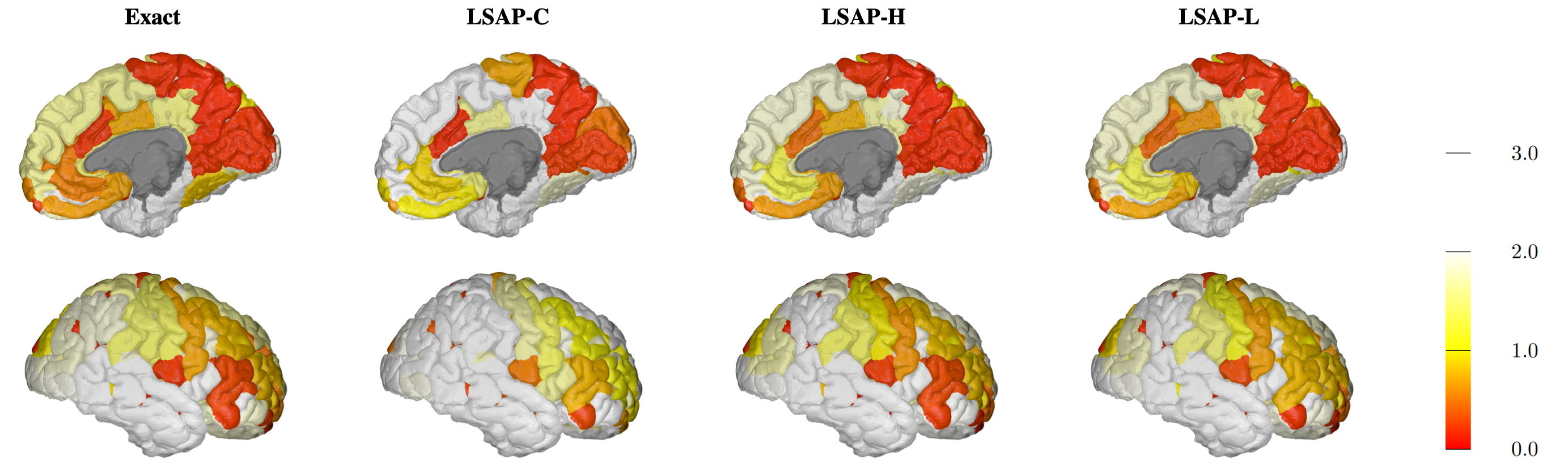
Localized Scales for Graph Classification

Figure: Visualization of the learned scales on the cortical regions of a brain. This visualization shows the scale of each ROI from the classification result using FDG feature. Top: Inner part of right hemisphere, Bottom: Outer part of right hemisphere.

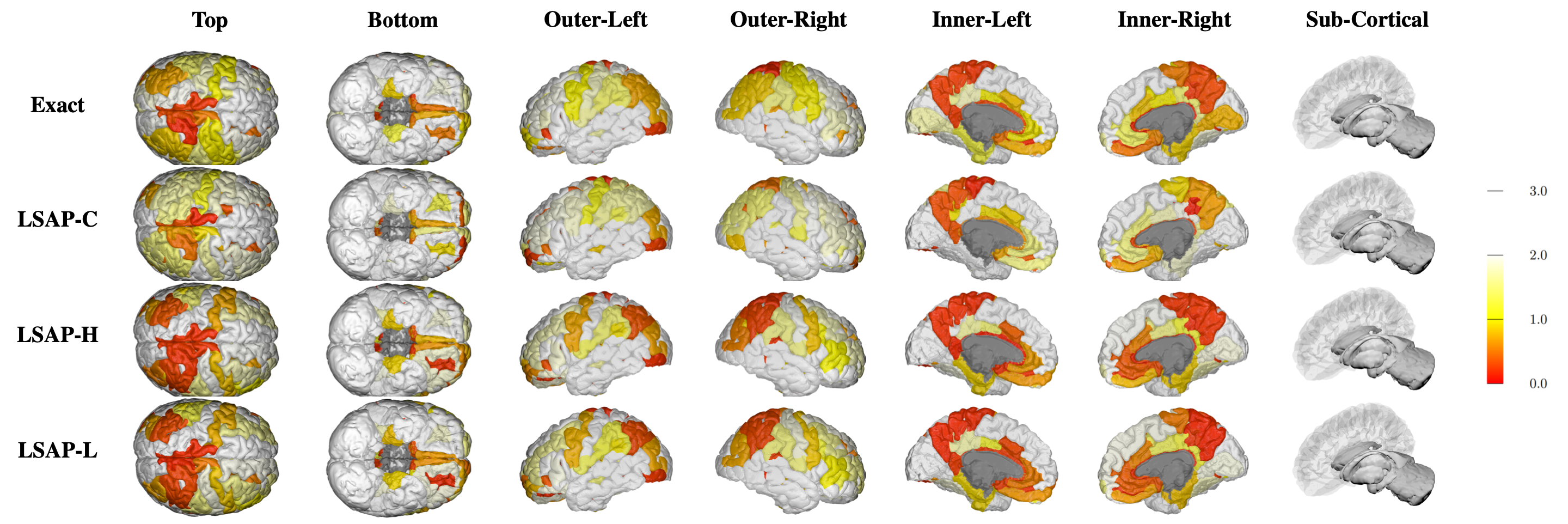
Figure: Visualization of the learned scales on the cortical and sub-cortical regions of a brain. This visualization shows the scale of each ROI through the classification result using Cortical Thickness feature.

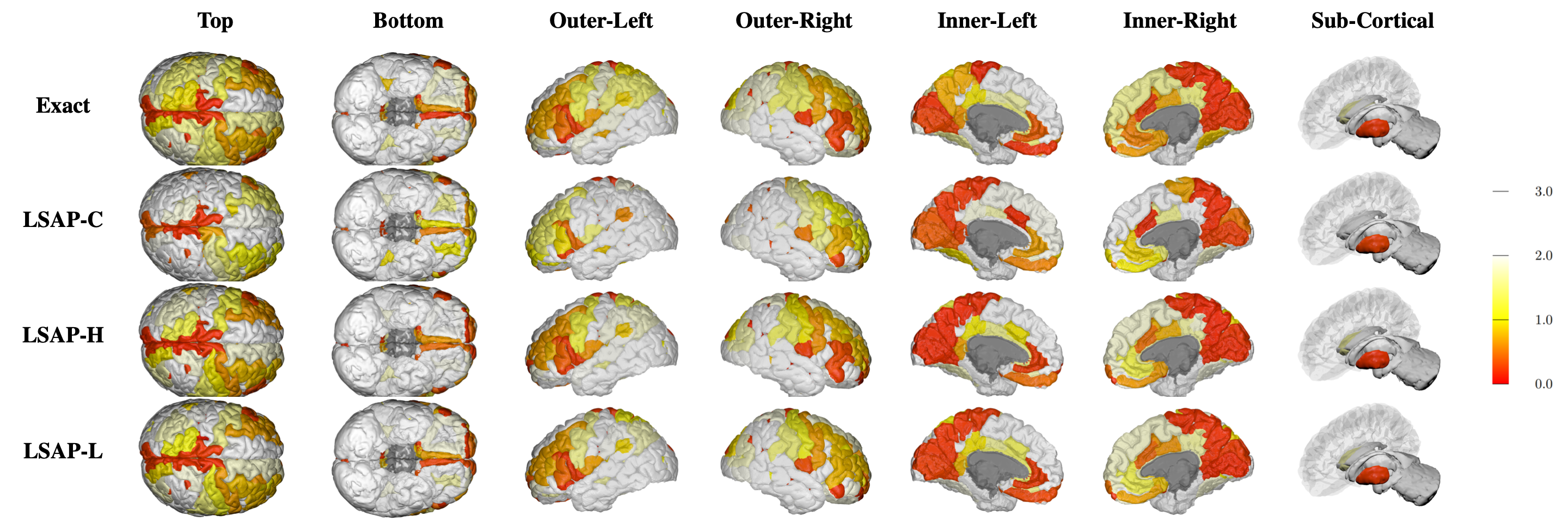
Figure: Visualization of the learned scales on the cortical and sub-cortical regions of a brain. This visualization shows the scale of each ROI through the classification result using FDG feature.

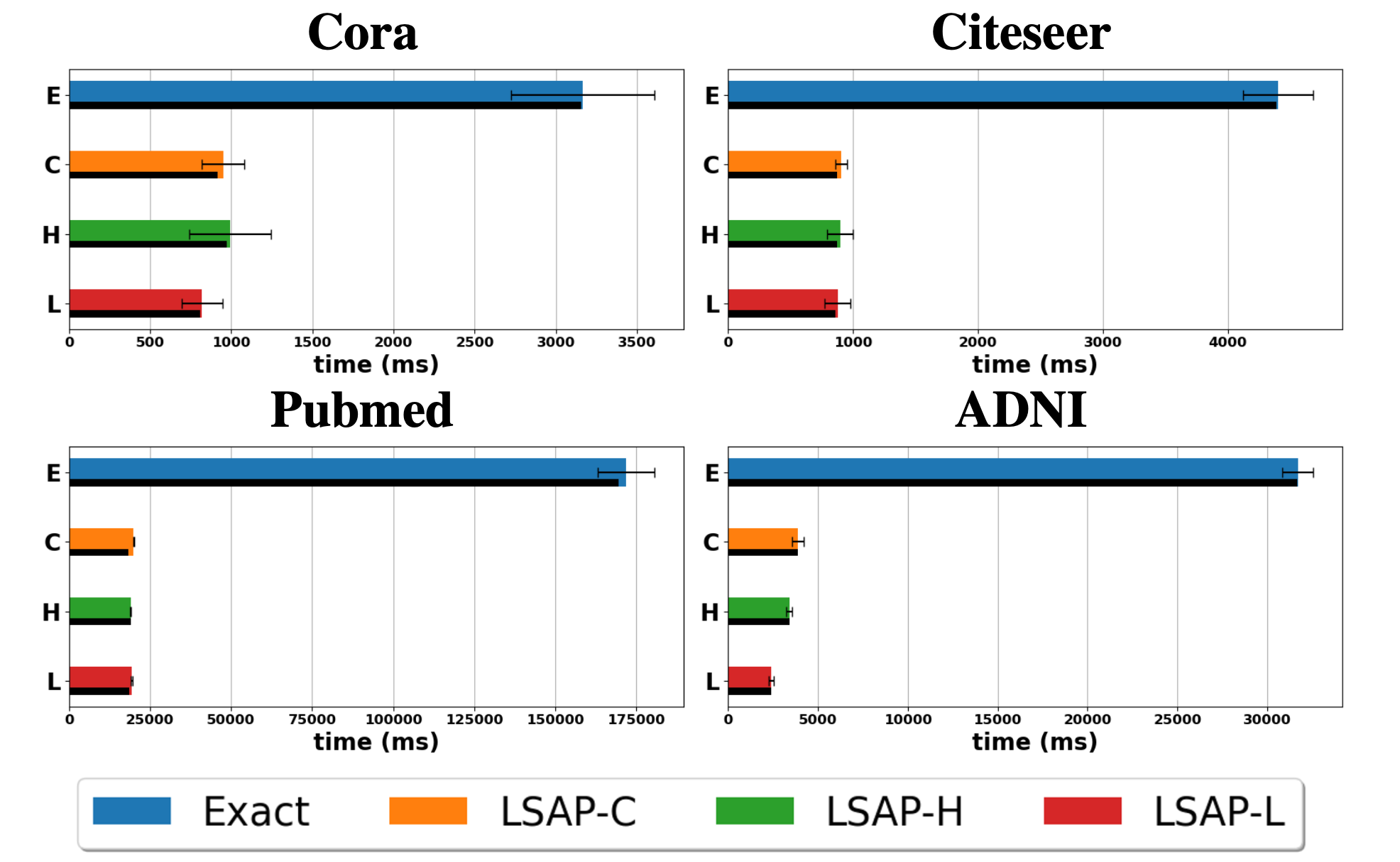
Computation Time with Kernel Convolution

Figure: Comparisons of computation time (in ms) for one epoch (Forward and backpropagation). Within the epoch, time for heat kernel convolution is given in black bar. Results were obtained from node classification and a graph classification with 10 repititions, and LSAP saves majority of the computation.

Conclusion

In this work, we proposed efficient trainable methods to bypass exact computation of spectral kernel convolution that define adaptive ranges of neighbor for each node. We have derived closed-form derivatives on polynomial coefficients to train the scale with conventional backpropagation, and the developed framework LSAP demonstrates SOTA performance on node classification and brain network classification. The brain network analysis provides neuroscientifically interpretable results corroborated by previous AD literature.

BibTeX

@inproceedings{sim2024learning,
    title={Learning to Approximate Adaptive Kernel Convolution on Graphs},
    author={Sim, Jaeyoon and Jeon, Sooyeon and Choi, InJun and Wu, Guorong and Kim, Won Hwa},
    booktitle={Proceedings of the AAAI Conference on Artificial Intelligence},
    volume={38},
    number={5},
    pages={4882--4890},
    year={2024}
}